Rob Napier

  • Externalizing properties to manage retains

    I have a very simple type in my system. It’s just an immutable struct:

    public struct AssetClass: Sendable, Equatable, Hashable, Comparable {
    public let name: String
    public let commodities: [String]
    public let returns: Rates

    public static func < (lhs: AssetClass, rhs: AssetClass) -> Bool {
        lhs.name < rhs.name
    }
    
    public static func == (lhs: AssetClass, rhs: AssetClass) -> Bool {
        lhs.name == rhs.name
    }

    public func hash(into hasher: inout Hasher) {
        hasher.combine(name)
    }
}

    It has a unique name, a short array of symbols that are part of this asset class, and a couple of doubles that define the expected returns. My system uses this type a lot. In particular, it’s used in the rebalancing stage of monte carlo testing portfolios. There are only 5 values of this type in the system, but they are used tens of millions of times across 8 threads.

    They’re value types. They’re immutable value types. So no problem. Except…

    Instruments output showing retain and release as over 50% of all time

    …

    ???

    Yes, across all threads, swift_retain and swift_release in this one function represent over half of my run time (wall clock, that’s about 12 seconds; the times here count all threads).

    But… structs. It’s all structs. Why? What?

    Most Swift Collections (Array, String, Dictionary, etc.) in most cases store their contents on the heap in a reference-counted class. This is a key part of copy-on-write optimizations, and it’s usually a very good thing. But it means that copying the value, which happens many times when it’s passed to a function or captured into a closure, requires a retain and release. And those have to be atomic, which means there is a lock. And since this value is read on 8 threads all doing basically the same thing, there is a lot of contention on that lock, and the threads spend a lot of time waiting on each other just for reference counting.

    In this case, none of the String values are a problem. Both the name and all the commodity symbols are short enough to fit in a SmallString (also lovingly called “smol” in the code). Those are inlined and don’t require heap storage.

    But that commodities Array. It’s small. The largest has 5 elements, and the strings are all 5 bytes or less. But it’s on the heap, and that means reference counting. And it isn’t actually used anywhere in the rebalancing code. It’s only used when loading data. So what to do about it?

    How about moving the data out of the struct and into a global map?

    public struct AssetClass: Sendable, Equatable, Hashable, Comparable {

    // Global atomic map to hold commodity values, mapped to asset class names
    // All access to `commodities` is now done through .withLock
    private static var commodityMap = OSAllocatedUnfairLock<[String: [String]]>(initialState: [:])

    public init(name: String, commodities: [String], returns: Rates) {
        precondition(Self.commodityMap.withLock { $0[name] == nil }, 
                     "AssetClass names must be unique: \(name)")

        self.name = name
        Self.commodityMap.withLock { $0[name] = commodities }
        self.returns = returns
    }

    public let name: String
    public var commodities: [String] { 
        Self.commodityMap.withLock { $0[name, default: []] }
    }
    public let returns: Rates
    // ...

    And just like that, 30% performance improvement. Went from 12s to 8s.

    This is a sometimes food. Do not go turning your structs inside out because Rob said it was faster. Measure, measure, measure. Fix your algorithms first. This slows down access to commodities, so if that were used a lot, this would be worse. And it relies on AssetClass being immutable. If there are setters, then you can get shared mutable state when you don’t expect it.

    But…for this problem. Wow.

    There’s more to do. Even after making this change, retain and release in this one function are still over 50% of all my runtime (it’s just a smaller runtime). But at least I have another tool for attacking it.

    Oh, and how did I know what kinds of objects were being retained? Try this as a starting point:

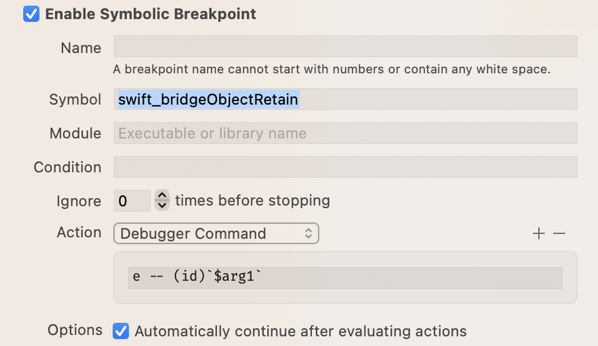
    Xcode breakpoint: Set symbol to swift_bridgeObjectRetain. Set action to Debugger Command, "e -- (id)`$arg1`" (resolve dollar-arg1 as an ObjC id), and Automatically continue.

    Be warned: this is a lot of output and very slow and the output is going to tell you about low-level types that may not have obvious correlation to your types, but it’s a starting point.

    OK, back to Instruments. I should definitely be able to get this under 5 seconds.

  • A short anecdote on getting answers on the modern internet

    This post is way off topic, and a bit in the weeds, and maybe even a bit silly, which is why I’m throwing it here rather than getting back to making my proper blog work. I really will do that, but… ok, not today.

    I’ve been trying to learn some abstract algebra. I never studied it in school, and sometimes I bump into people describing operations in “group-speak” (throwing around words like “abelian” and “symmetric group”), and I’d like to try to keep up with what they’re saying even if I probably will never do an actual proof in anger.

    Anyway, I got myself confused about the meaning of “order” when talking about groups vs elements. It’s the kind of dumb “how could you not know this at this point in the course?” question that you’re embarrassed to ask (and so I blog about it because I have an under-developed sense of shame). So… let’s ask some LLMs! And also search engines. And how would I figure this out?

    Good news: it took longer to write this up than to fix my misunderstanding. OK news: nothing lied to me (well, much). Bad news: well, we’ll get to that as it comes up.

    Here’s the exact text I stuck into a bunch of things:

    Is the order of a group the lcm of the order of its elements?

    To be clear to anyone who knows abstract algebra: I was confused and thought this might be the definition of order. I was misunderstanding the point of Lagrange’s theorem. To anyone who doesn’t know abstract algebra, the correct answer is just “the number of elements in the group.” It really is that simple, and I was making it really over-complicated.

    Kagi

    Kagi has become my go-to search engine. I like the model of “I pay you, and you provide a service, that’s it, that’s the whole business model.” It gave me several links that weren’t particularly useful (basically ones that prove Lagrange’s theorem, which assume you already know the answer to my question).

    But the third link was to a Saylor Academy text book, which answered my question:

    In group theory, a branch of mathematics, the term order is used in two closely-related senses:

    • The order of a group is its cardinality, i.e., the number of its elements.

    • …

    OK, that’s cleared up.

    Am I done? Of course not! I had to dig through three or four links, most of which confused me more, before I finally found the link to an open-source textbook, where I could go double-check the definition. The internet should be better than that!

    Other search engines

    To quickly summarize other search engines (because you’re all familiar with those, and of course the point is to get to LLMs):

    • Duck Duck Go – (OK) Second link was Wikipedia, which gives the answer in the first sentence. For completeness, searching for the same question on Wikipedia directly also gets you right to the page.

    • Google – (Bad) The Q&A section gives several links to different questions on Stack Exchange, Quora, and Studysmarter.us (?). Importantly, the second answer Google highlights is excerpted as: “Yes, in fact, the order of an element in a finite group…” (The “…” is in the Google excerpt.) You have to carefully notice that this is the answer to a different question. If you read quickly, you could easily walk away thinking “yes” is the answer. This is a big problem with search engine excerpting IMO. If you scroll down past the Q&A section, the first (unrelated) math.stackexchange answer, the “People also ask” section, and then two more links, you will finally come to the Wikipedia article that does answer the question and is where I should have started anyway.

    • Bing – (Good!) The highlighted answer links to Math.SE, and is extremely useful. It provides this directly on the search page:

    No. For instance if G = Z2 ⊕ Z2, then | G | = 4, but the least common multiple of the order of it’s group elements is 2.

    Bing added the bold on “No.” This is the only search that directly answered my question, with citation, in one step. The Math.SE link is a bit funny, though. Five years ago, someone had almost exactly the same question as I did. It was answered in a couple of useful ways, had an accepted answer, and then was closed as off-topic. (!?!?!) This question does not show up in most web searches (other than Bing) and does not show up (at least not prominently) when I put my search directly into math.se.

    Bing definitely won this one. Also, of course, just going to Wikipedia.

    The LLMs - Bing

    OK, but we all know what this was really about. How do the LLMs handle this kind of question? Well, let’s start with Bing, since it answered the question so well through search.

    Me: is the order of a group the lcm of the order of its elements?

    Bing: No, the order of a group is not necessarily the least common multiple of the order of its elements. For instance, if G = Z2 ⊕ Z2, then |G| = 4, but the least common multiple of the order of its group elements is 2.

    Precisely the same answer as in the “quick answer” from search, except this time it’s plagiarism. It is word-for-word the answer from Aweygan on math.se, but gives no link, citation, or even hint that this isn’t original content.

    Maybe I could get the citation by asking?

    Me: What’s the source of your answer?

    Bing: My answer is based on my internal knowledge and information. I am programmed to provide accurate and reliable information to the best of my ability.

    O_o

    Yeah.

    ChatGPT

    And of course I must check ChatGPT:

    No, the order of a group is not necessarily the least common multiple (lcm) of the orders of its elements.

    The order of a group is the number of elements in the group. On the other hand, the order of an element in a group is the smallest positive integer n such that the element raised to the nth power is the identity element of the group.

    Hey, that’s actually really good. Just the right about of extra information. I’d like citations of course, but just being right about basic facts without plagiarism is pretty good (after all, the math.SE answer doesn’t provide citations, either). I like this. This is good.

    And it goes on:

    It is true that the order of an element divides the order of the group, by Lagrange’s theorem. However, the lcm of the orders of the elements may be larger than the order of the group. For example, consider the cyclic group of order 6 generated by a. The group contains elements of orders 1, 2, 3, and 6. The lcm of these orders is 6, but the order of the group itself is only 6.

    Therefore, the order of a group cannot be expressed in terms of the lcm of the orders of its elements, in general.

    Ah, a counter-example where the lcm is larger than the order. Very helpful. In the case where the order is six and the lcm is…six?

    Oh ChatGPT. If only you’d quit while you were ahead.

  • A Reminder About NSRange and String

    The NSRange for a full string is NSRange(location: 0, length: (text as NSString).length). You cannot use text.count for this. NSRanges on strings are based on UTF-16 code points, not Swift Characters. A character like 👩‍👩‍👧‍👧 has a .count of 1, but a .length of 11. ObjC-based NSRange APIs (even ones ported to Swift) need the latter. Swift interfaces (which use Range rather than NSRange) need the former.

    Whenever possible, avoid NSRange. But when it’s needed, make sure to use it correctly. It’s very easy to make mistakes that break on non-ASCII, and especially on emoji.

    (Side note: (text as NSString).length is the same as text.utf16.count. I don’t have a strong opinion on which to use. In both cases, future developers may get confused and try to “fix” the code back to text.count. (text as NSString) is nice because it ties it back to this being an NSString API and is easier IMO to see that something special is happening here, but it also looks like an auto-conversion barnacle. .utf16.count is shorter and calls out what is really happening, but I almost always type .utf8.count out of muscle-memory and it’s hard to see the mistake in code-review. So do what you want. A comment is probably warranted in either case. I hate NSRange in Swift…)

subscribe via RSS